I've recently become interested in using Lean for some projects, both in research and in teaching. This Fall I'm teaching a category theory class (with John Li), so it seemed natural to try to write down some definitions in category theory in the proof assistant to prepare for the class, evaluate its efficacy as a potential teaching tool, and learn some Lean at the same time. This post (series of posts?) is written from the perspective of a first-time Lean user, so some choices may be suboptimal. A full listing for all the code discussed in this article can be found at this Gist.

Let's start by defining a category. There's a surprising lack of clarity and precision in the typical definition of a category found in many textbooks, in my opinion. One of the benefits -- and, occasionally, pitfalls -- of working in a proof assistant is that there isn't any room for ambiguity in these definitions. Here is the definition of a (small) category in Lean, borrowed from mathlib:

class SmallCategory (ob : Type) : Type 1 where
  hom : ob → ob → Type
  id : ∀ x, hom x x
  comp : ∀ {X Y Z}, hom X Y → hom Y Z → hom X Z
  id_comp : ∀ {X Y} (f : hom X Y), comp (id X) f = f
  comp_id : ∀ {X Y} (f : hom X Y), comp f (id Y) = f
  assoc : ∀ {W X Y Z} (f : hom W X) (g : hom X Y) (h : hom Y Z),
    comp (comp f g) h = comp f (comp g h)

infixl:65 " ⟶ " => SmallCategory.hom
notation:65 a:64 " ∘ " b:65 => SmallCategory.comp b a

There are several things of note about this definition, which each deserve some discussion.

• Categories are typeclasses. This means that we can use typeclass inference and resolution to flexibly and implicitly convert data into categories and reason about their properties. We'll see examples of why this is useful.
• The objects of categories are elements of Type. The Type type in Lean can be thought of as the type of Lean programs. For instance, Bool is an inhabitant of Type, as is the function Bool -> Bool. This means we can define categories on objects that are themselves Lean programs, and use category theory to prove properties about those programs. I find [this reference] quite helpful on this notion, and we'll see some examples.
• The definition of hom is ob → ob → Type: given two objects of the category, they are related by a Lean program. We will write this as \(A \xrightarrow{f} B\) where \(A\) and \(B\) are objects and \(f \in \texttt{hom}(A,B)\). This notion is best illustrated with examples, which we'll see soon.
• For every object \(A\) there is a morphism \(A \xrightarrow{\texttt{id}} A\) called the identity morphism.
• comp says that if there are morphisms \(A \rightarrow B\) and \(B \rightarrow C\), then there is a morphism \(A \rightarrow C\)

The remainder of the properties of categories that describe how morphisms must behave:

• id_comp and comp_id dictate that the identity morphism must behave like an identity by leaving any morphism composed with it unchanged
• assoc states that composition of morphisms is associative

Instantiating the Category class

At this point it's best to see some concrete examples so that we can get a sense for how this definition behaves. We will instantiate progressively more interesting instances of categories, encountering more features of Lean and more exotic kinds of categories as we go.

Integers mod 2

Our first simple example of a category is integers modulo 2. The first step in defining a category in our setup is to give the type of its objects. This category has a single object, which we denote as Star. The type Star is an element of Type, and it has a single inhabitant: the star type constructor.

inductive Star
| star

If you're familiar with it, you would recognize this definition: it's the definition of the Unit type.

Next we need the type of morphisms for our category. There are exactly two morphisms: `add_0` and `add_1`. We can describe these as a Lean inductive:

inductive AddZ_2
  | add_0
  | add_1

Now we are ready to instantiate our SmallCategory typeclass:

instance CatZ_2 : SmallCategory Star where
  hom _ _ := AddZ_2
  id _ := .add_0
  comp f g :=
    match (f, g) with
    | (.add_0, .add_0) => .add_0
    | (.add_1, .add_0) => .add_1
    | (.add_0, .add_1) => .add_1
    | (.add_1, .add_1) => .add_0
  id_comp := by grind
  comp_id := by grind
  assoc := by grind

Some notes about this definition:

• Since there is only a single object the definition of hom is simple: the star object can be related to itself in one of two ways: either by adding 0 or by adding 1. Convince yourself that this typechecks with our definition of a category.
• The identity is defined to be the add_0 morphism
• The most interesting definition is comp. Here is where you see the actual structure of addition modulo 0 unfold: adding 0 and 0 is the same as adding 0, adding 1 and adding 0 is the same as adding 1, etc.

The properties of morphisms can all be dispatched to the fancy grind tactic that proves them quickly. We could of course prove these without grinding. For instance let's prove id_comp without grind:

instance CatZ_2 : SmallCategory Star where
  hom _ _ := AddZ_2
  id _ := .add_0
  comp f g :=
    match (f, g) with
    | (.add_0, .add_0) => .add_0
    | (.add_1, .add_0) => .add_1
    | (.add_0, .add_1) => .add_1
    | (.add_1, .add_1) => .add_0
  id_comp := by
    ...

This yields the proof state:

⊢ ∀ {X Y : Star} (f : AddZ_2),
  (match (AddZ_2.add_0, f) with
    | (AddZ_2.add_0, AddZ_2.add_0) => AddZ_2.add_0
    | (AddZ_2.add_1, AddZ_2.add_0) => AddZ_2.add_1
    | (AddZ_2.add_0, AddZ_2.add_1) => AddZ_2.add_1
    | (AddZ_2.add_1, AddZ_2.add_1) => AddZ_2.add_0) =
    f

Always take a moment to stare at your proof goal before hammering out tactics. This is a "proof by computation": we need to show that running our definition of hom with id for the first argument and some morphism f for the second argument always yields f again. Proofs by computation, especially simple ones, usually involve only a few tactics:

• simp, which performs beta reduction and runs your program;
• rfl which ends the proof by checking for definitional equality. rfl does quite a bit more than this: it flexibly uses any reflexivity lemma tagged [@refl], which can enable it to deduce some surprisingly definitional equalities sometimes.
• cases which performs case analysis on inductives by breaking them up into their constructors;
• and of course intro to eliminate the $\forall$ quantifiers.

Indeed we can prove this using these tactics:

id_comp := by
   intro X Y f
   cases f <;> rfl

In this case, we can use the tactic sequencing combinator <;> to apply the rfl tactic to the goal generated by calling cases on f. Note that rfl here is doing some additional simplification beyond simply checking definitional equality.

Poset category

Our next example is more interesting because it gives a much more generic construction of a category: we will show how to define an instance of the SmallCategory typeclass for any data that behaves like a partially ordered set (poset). Defining categories in this way is very typical in mathematics, so it's quite useful to see how our encoding in Lean handles this.

First we define the Poset typeclass:

class Poset (α : Type) where
  le : α → α → Prop
  reflex: ∀ x, le x x
  transitive: ∀ x y z, le x y → le y z → le x z
  antisymmetric: ∀ x y, le x y → le y x → x = y

infixl:65 " ≤ " => Poset.le

The le relation is a map α → α → Prop. The Prop type in Lean is the type of propositions.

Now we can give a SmallCategory typeclass instance for any type \(\alpha\) that satisfies the Poset typeclass constraint:

instance PosetCategory P [Poset P] : SmallCategory P where
  hom a b := PLift (a ≤ b)
  id a := ⟨ Poset.reflex a ⟩
  comp { a b c } f g := ⟨ Poset.transitive a b c f.down g.down ⟩
  id_comp := by grind
  comp_id := by grind
  assoc := by grind

This definition is our first encounter with Lean's universe hierarchy management facilities. Some notes about this definition:

• According to the lean docs, "`PLift` can lift any type, including propositions, by one level". Since hom expects its codomain to be at Type 0, we need to use PLift to raise the le relation (since Prop) is Sort 0. This is an instance where Lean's pedantic universe hierarchy plumbing gets in the way of the clarity of our definitions, but it's not too bad.
• The ⟨ Poset.reflex a ⟩ macro-expands to PLift.up (Poset.reflex a). Think of this as "constructing an inhabitant of PLift (a ≤ b)".
• Composition of morphisms follows by lifting the transitive property of the relation, and the rest by grind (which are again simple calculational proofs).

This may all seem very confusing. Universe hierarchy management is probably the most annoying aspect of embedding category theory into a proof assistant. Most traditional presentations rely on "naive set theory" as an ambient logic for stating definitions about categories, and consequently most basic treatments of category theory avoid mentioning universe hierarchies until they absolutely must (i.e., once they reach categories of larger cardinality), and even then, these issues of universe hierarchy are usually swept under the rug.

Overall I haven't found working with universe hierarchies too bad in Lean; one mostly "follows the types", and once a term typechecks, it's OK.

Endomaps on sets

Now for an even more interesting definition of category: one with a more interesting definition of morphism.

The category of endomaps on finite sets has objects that consist of (1) a finite set over \(s \in \alpha\), and (2) a map \(m : s \rightarrow s\). You can think of this category as behaving similar to finite automata: the states of the automata are \(s\), and the map \(m\) describes the transitions taken by the system.

We can define the type of objects as follows (making use of mathlib's definition of finite sets):

structure Endoset α where
  s : Finset α
  map : s → s

We can draw objects of this category as:

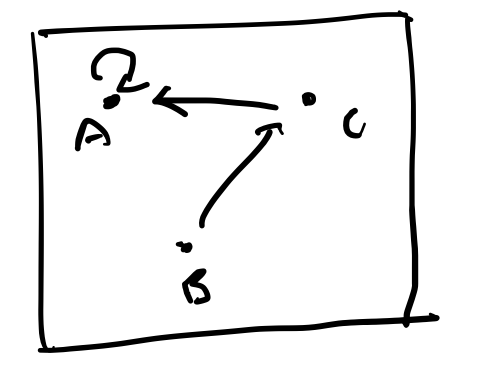
Here we've drawn the elements of the set as points \(\{A,B,C\}\) and the map of the set using arrows.

The morphisms of this category are special: they will behave like automata refinements. Concretely, a morphism \((A, \alpha) \xrightarrow{f} (B, \beta)\) is a set-function \(f : A \rightarrow B\) paired with a proof that \(f \circ \alpha = \beta \circ f\). Here is an example of a valid morphism, with the morphism drawn in red:

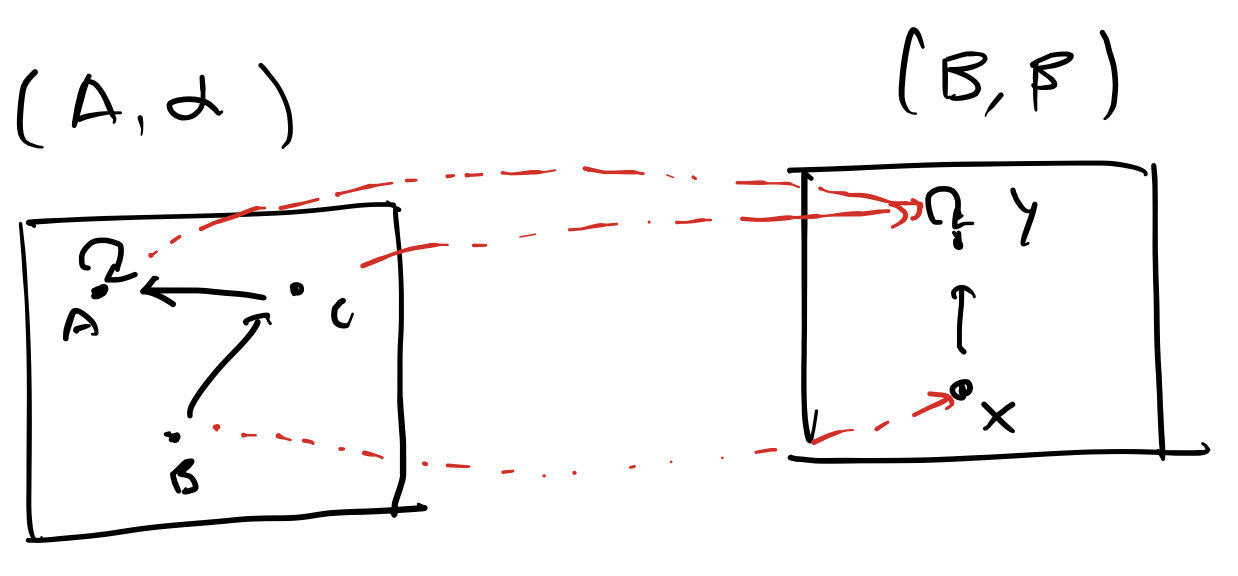
In category theory, this sort of morphism is often referred to as a diagram. We can write down the definition of this category as follows:

instance EndoCat : SmallCategory (Endoset α) where
  hom a b := {}
  id a := ⟨ fun x => x, by rfl ⟩
  comp f g :=
    ⟨ g.val ∘ f.val, by
      cases f
      rename_i fv propf
      cases g
      rename_i gv propg
      simp
      conv =>
        lhs
        rw [Function.comp_assoc]
        rw [propf]
        rw [<- Function.comp_assoc]
        rw [propg]
      rfl⟩

  id_comp := by aesop
  comp_id := by aesop
  assoc := by aesop

As usual, this definition introduces us to a few more Lean features that we briefly explain here:

• The notation {f : a.s -> b.s // f ∘ a.map = b.map ∘ f } denotes a subtype. A subtype {x : a // p x} denotes the collection of all elements x of type a for which p x is true, where p is some proposition on a.
• An inhabitant of subtypes is a pair ⟨ f, pf ⟩ where f has type a and pf is a proof that f satisfies the required predicate.
• The definition of comp is quite interesting: this is essentially a "diagram chasing argument". The interested reader should step through this definition to see how it works; I've left the proof quite verbose so it's easy to see the logic.

Conclusion

I found writing these definitions and carefully translating them into Lean highly interesting and educational as a way of more deeply understanding Lean (in particular its way of managing universe hierarchies and typeclasses). It was also surprisingly useful for understanding category theory.